Speed Snek: Drawing the Snek

This is a post about the development of Speed Snek. In the game of Speed Snek, the snek segments are drawn using solid links (like an articulated bus!). I need to figure out how to place these solid line segments along the user's input, which will be a squiggly line drawn using a finger or pointer.

The general process

Here's how I plan to implement it.

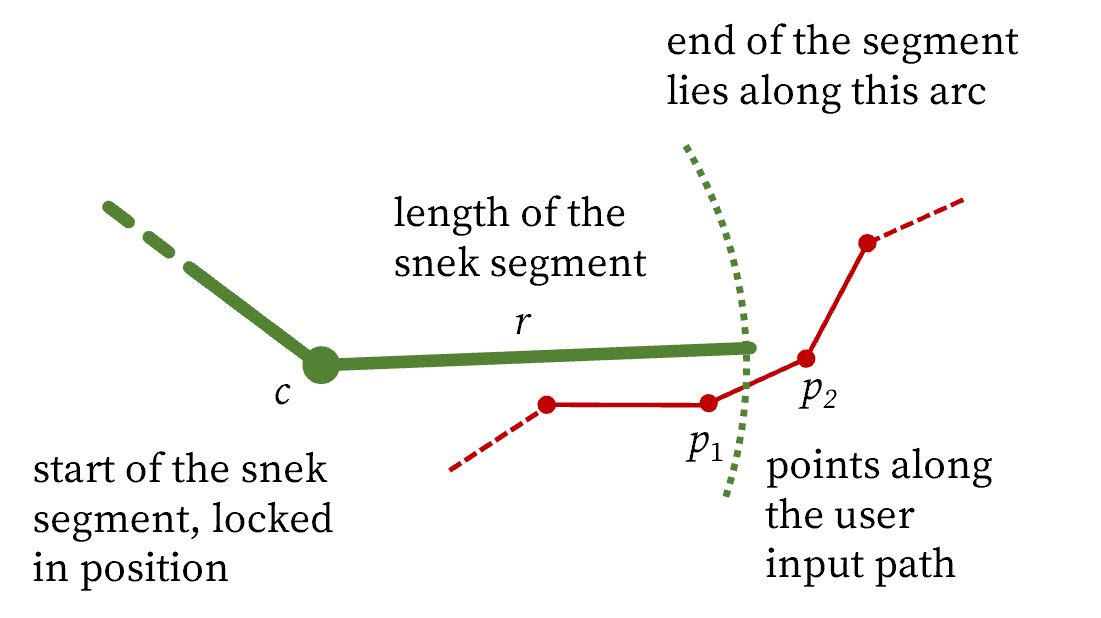
Model used during calculation of the snek segment placement

  1. Fix the beginning of the snek segment cc to either the user's finger/pointer (for the first segment) or the end of the preceding segment (for all other segments)
  2. Go down the user's input path (implemented as a list of canvas coordinates) until it reaches a point on the path that cannot be reached by the current snek segment (p2p_2). The end point of the segment must lie on the line drawn between that point and the previous point p1p_1.
  3. Figure out where on the line (p1,p2)(p_1, p_2) the end of the segment will lie.
  4. Trim the user input path data, so unnecessary path data isn't being stored in memory.

If all goes well, the snek should follow the user's input, with all articulation points falling on the input path like so:

Sketch of expected outcome, with the solid links of the snek following the user's input

The math

As seen in the figure above, it comes down to figuring out the intersection of the line segment determined by p1:(x1,y1)p_1: (x_1, y_1) and p2:(x2,y2)p_2: (x_2, y_2) with the circle of radius rr centered at c:(xc,yc)c: (x_c, y_c).

The points (x,y)(x, y) on the segment can be defined parametrically by

{x=tx1+(1−t)x2y=ty1+(1−t)y2\begin{equation} \begin{cases} x &= tx_1 + (1-t)x_2 \\ y &= ty_1 + (1-t)y_2 \end{cases} \end{equation}

where 0≤t≤10 \leq t \leq 1. Since the distance between this point and cc must be rr, we can use the Pythagorean theorem to get the equation

r2=(tx1+(1−t)x2−xc)2+(ty1+(1−t)y2−yc)2\begin{equation} \begin{split} r^2 = &(tx_1 + (1-t)x_2 - x_c)^2 \\ &+ (ty_1 + (1-t)y_2 - y_c)^2 \end{split} \end{equation}

This can be cleaned up into a quadratic equation for tt

0=((x1−x2)2+(y1−y2)2)t2+2[(x1−x2)(x2−xc)+(y1−y2)(y2−yc)]t+(x2−xc)2+(y2−yc)2−r2\begin{equation} \begin{split} 0 = &((x_1 - x_2)^2 + (y_1 - y_2)^2) t^2 \\ &+ 2[(x_1 - x_2) (x_2 - x_c) + (y_1 - y_2) (y_2 - y_c)] t \\ &+ (x_2 - x_c)^2 + (y_2 - y_c)^2 - r^2 \end{split} \end{equation}

That's the quadratic formula, I know how to solve that! And so...

t=−b±b2−4ac2a t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

where

a=(x1−x2)2+(y1−y2)2b=2(x1−x2)(x2−xc)+2(y1−y2)(y2−yc)c=(x2−xc)2+(y2−yc)2−r2\begin{align} a &= (x_1 - x_2)^2 + (y_1 - y_2)^2 \\ b &= 2(x_1 - x_2) (x_2 - x_c) + 2(y_1 - y_2) (y_2 - y_c) \\ c &= (x_2 - x_c)^2 + (y_2 - y_c)^2 - r^2 \end{align}

It's not pretty, but it shouldn't be too difficult to implement. The value of tt can then be plugged back into (1) to get the end point for the segment. Of course a quadratic formula can give us two answers, but we only care about cases where 0≤t≤10 \leq t \leq 1. What about if both values of tt match the range? Well, that's a problem for future me.